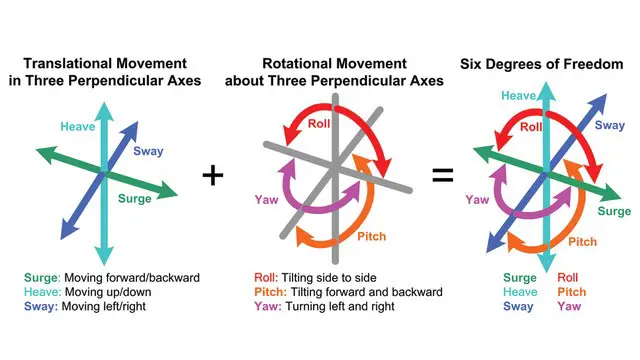
Degree of freedom is defined as the minimum number of independent variables required to define the position or motion of a system is known as degree of freedom. It is the property of kinematic chain which shows that in how many directions the connected links of the kinematic can move freely. It is also known by mobility.
Degree of Freedom:
In 3-D space system an unconstrained rigid body possesses six degree of freedom. Total number of motions in space is six as 3 are rotary and 3 are translatory along x, y and z axis respectively. Here DOF can also be defined as the subtraction of total number of motions and the number of motions restraints or arrested (those motions which are not possible).
DOF = 6 – Restraints
ALSO READ: What is Gyroscope
In 2-D space system maximum 3 motions can be predicted as 2 translatory motion along x and y axis respectively and 1 rotary in perpendicular to x-axis i.e. z-axis.
DOF = 3 – Restraint
To determine DOF of 2-D planar mechanism, Kutzback was a scientist who gave the relation
DOF = 3(L-1) – 2j – h
where,
L = number of links
j = number of joints
h = number of higher pairs
Sometimes a system may have one or more links of a mechanism which do not introduce any extra constraint, such links are known as redundant links and should not be counted to find the DOF and also corresponding joint will not be counted.
Sometimes one or more links of a mechanism can be moved without causing any motion to the rest of the links of the mechanism, such a link is said to have redundant DOF. Due to this DOF formula for planar mechanism is modified.
DOF = 3(L-1) – 2j – h – Fr
where,
Fr = redundant motion
Now Grubler was another scientist, he utilized the Kutzback equation and gave his formulation i.e. he used the equation and put DOF equal to 1 and higher pair equal to zero for a kinematic chain. Grubler’s criterion was the extension of Kutzback equation and expressed as
DOF = 3(L-1) – 2j – h
1 = 3(L-1) – 2j – 0
3L – 2j – 4 = 0 (this is the derived equation of Grubler’s criterion.)
From Grubler’s criterion it is clear that to hold the equation number of links should be even i.e. minimum number of links required is 4.
This is all about degree of freedom. If you have any query regarding this article, ask by commenting. If you like this article, don’t forget to share it on social networks. Subscribe our website for more informative article. Thanks for reading it.