We know about fatigue and feel it many times in our body after long workout. Similarly engineering components are also fails due to fatigue. Fatigue failure in any engineering component occurs when these components are subjected to cyclic loading or we can say that the fluctuating stresses are induced in the components. Fatigue is the time dependent permanent deformation which is seen in almost every engineering component when they work under cyclic loading conditions.
Most of the time the engineering components are fails only because of fatigue. During the cyclic loading the deformation develops on the microscopic level and this very small defect grows until a macroscopic crack is formed. As time goes on this microscopic crack grows for each cycle until it reaches a critical length. When the same load is repeated without any precaution then the cracked component breaks because it cannot sustain the peak load for longer time. This damage occurs in the component which is known as fatigue. In mechanical components the most of the time failure occurs due to the fluctuating stresses which is the case of the fatigue failure.
Fatigue Failure:
Fluctuating stresses:
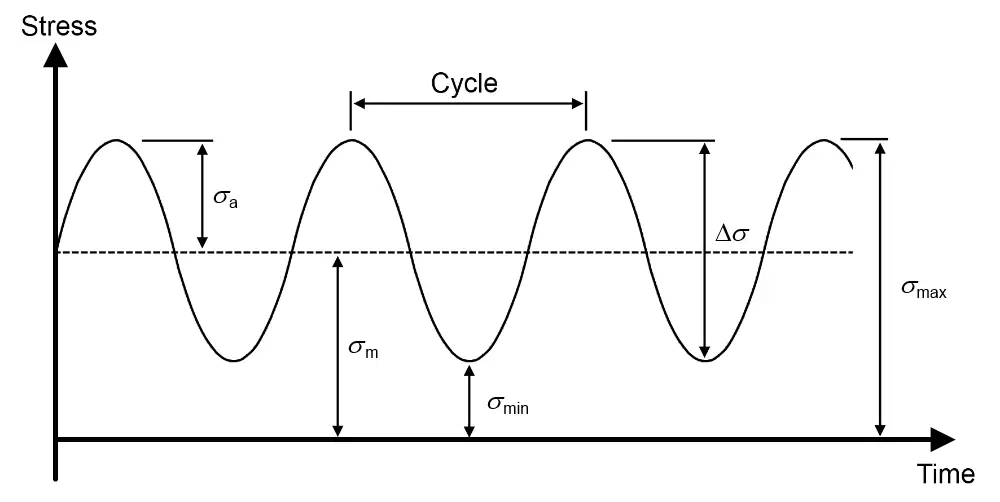
Fluctuating stresses are the cause of the fatigue failure. The stress magnitude is lower than the ultimate tensile strength of the material. Engineering components are subjected to external force which is not static in nature whose magnitude is changing with respect to the time and the stresses induced by these forces are termed as fluctuating stresses. The fluctuating in any mechanical component is easily understood by the help of sine wave curve.
The variations of the stresses are categorized in three types which are Fluctuating stresses, Repeated stresses and Reversed stresses. The sine wave is constructed in between stress and time. The fluctuating or alternating stress is varying in sinusoidal form with respect to the time. The fluctuating stress has two values i.e. minimum and maximum which is easily understood with the help of diagrams. The stress varies from zero value to the maximum value. In the calculation of the fluctuating stresses the tensile stress is considered as positive and compressive stresses are negative. The mean stress and the amplitude of the stress can be easily calculated by the help of following formulas.
σm = (σmax + σmin)
σa = (σmax – σmin)
σm is the mean stress and σa is the stress amplitude. σmax and σmin are the maximum and minimum stresses respectively.
In case of Repeated stress the value of minimum stress is zero i.e. σmin = 0 and in Reversed stresses the mean stress is zero i.e. σm = 0.
Failures due to fatigue:
Sometime we use this method to cut the wire by bending and unbending for few times. The cyclic repeated force cause failure and wire break in two pieces. This is the very common example of the fatigue failure. The fatigue failure is defined as the time dependent fracture under cyclic loading. The fatigue failure is different from the static failure. The region of the crack is subjected to the stress concentration. This crack is elongated due to the cycling loading conditions of fluctuating stresses as a result in the form of deformation of the engineering components.
The fatigue or endurance limit describes the life of the mechanical component which is defined as the maximum amplitude of completely reversed stress that the standard component can sustain for an infinite number of cycles without the fatigue failure. The fatigue life is another term which is used with the endurance limit for better understanding of the life of the components. It is defined as the number of stress cycles that a standard component can completed during the test before any crack appears. If the value of the induced stress in the component is less than or equal to the endurance limit than the component has infinite life (≥ where as if the value of the induced stress is greater than endurance limit than the component has finite life ( to cycles ).
This is basic about Fatigue. If you have any query regarding this article, ask by commenting. If you have like this article, don’t forget to share it on social networks. Subscribe our website for more informative article. Thanks for reading it.