Theory of failure describe the elastic failure of the mechanical components. At the time of working machine components subjected to various loads which cause different types of stress in it. Theories of failure help us to determine the safe dimensions of the machine components when they are subjected to bi-axial or tri-axial state of stresses. Any component is failed if the induced stress exceeds the elastic limit and permanent deformation of the component takes place. The failure in the materials is of two type i.e. brittle failure and ductile failure. In brittle failure the direct separation takes place without any kind of appreciable elongation whereas in ductile failure we can see appreciable inelastic elongation before the failure. Both types of failure depend on the type of material by which machine component is made.
All the mechanical components failed when elastic limit is reached to a certain value and yielding starts. Different theories have been proposed for different materials and failures. These theories are used to obtain the relationship between stresses induced under bi-axial and tri-axial state of stress conditions and the material properties which are obtained by the tension test or compression test. These properties are Sut (ultimate strength in tension), Syt (yield strength in tension) and so on. The yielding in the material depends upon the several stress components. The failure of any mechanical part depends upon various factors like properties of material, type of loading and temperature etc. for example a power screw subjected to torsional moment as well as axial force, an overhang crank is subjected to combined bending and torsional moment, same in the case of bolts of the bracket which are subjected to forces that causes tensile stress and shear stress, where as crank shafts and connecting rods are examples of the those components which are subjected to complex loads.
Before designing of any machine part several experiments are performed on them to obtain safe working stress under combined loading conditions. These experiments help us to determine the different properties of the materials under similar loading conditions. But sometimes it is not possible to perform these tests for different possible combinations of load to obtain mechanical properties. Generally most of the mechanical properties of any component are obtained by tension test which is performed on UTM (Universal Testing Machine). These properties are yield strength, ultimate tensile strength and percentage of elongation. Theories of failure give a relationship between the strength of machine component which are subjected to complex state of stresses with the mechanical properties which are obtained during the tension test. Following are the key points which are helpful in better understanding of theories of failure:-
- σ1, σ2 and σ3 are the principle stresses induced at a point on the machine part in three mutual perpendicular directions due to the different loading conditions. We use different theories to obtain the relationship between σ1, σ2 and σ3 with the material properties like Syt (yield shear strength in tension), Sut (ultimate strength in tension), Sys (yield strength in shear) and factor of safety FOS (N).
- Under uniaxial state of stress condition i.e. only σ1 is acting on the machine component then the strength criterion and all theories of failure will give the same result so we have no requirement of theory of failure in case of uniaxial state of stress condition.
- In case of bi-axial and tri-axial state of stress conditions all the theories of failure will provide different results. So for the safe design of any component under bi-axial and tri-axial state of stress condition appropriate theory of failure should be selected.
- Under bi-axial and tri-axial state of stress conditions all the theories of failure provide almost same result when σ1 is very large as compared to the σ2 and σ3.
Theory of Failure:
Different theories are proposed by considering the different stresses such as the maximum principle stress, the maximum principle strain, the maximum shear stress, the maximum strain energy and the maximum shear strain energy. By using these stresses different hypothesis of failure were made. According to these, following are the commonly used five theories of failure.
- Maximum Principle Stress Theory (Rankin’s Theory)
- Maximum Principle Strain Theory (Saint Venant’s Theory)
- Maximum Shear Stress Theory (coulomb, Tresca and Guest’s Theory)
- Total Strain Energy Theory (Haigh’s Theory)
- Maximum Shear Strain Energy Theory or Maximum Distortion Energy Theory (Huber Von Mises and Hencky’s Theory)
1. Maximum Principle Stress Theory:
This theory was proposed by W.J.M Rankin. This is one of the oldest and simple theories. According to this theory the failure in the mechanical component takes place when they are subjected to bi-axial or tri-axial state of stress and then the value of maximum principle stress reaches the yield strength or ultimate strength of the material. In this theory only maximum principle stresses are consider, rest all the principle stresses have not any influences on it. If we consider three principle stresses σ1, σ2 and σ3 at a point on a machine component then σ1 > σ2 > σ3.
The condition of the failure is,
σ1 = Syt or σ1 = Sut
Maximum principle stress theory is considered as the best theory of failure for brittle materials, but it is also suitable for ductile materials under the following state of stress conditions:-
- Uniaxial state of stress condition only
- Bi-axial state of stress condition when principle stresses are like in nature. Here σ2 is neglected because of unlike nature.
- Hydrostatic state of stress condition i.e. when σ1 = σ2 = σ3.
GRAPHICAL REPRESENTATION:
A square represents the state of stresses under this theory. Square is divided into four quadrants i.e. in first quadrant both σ1 and σ2 are positive or tensile in nature. In second quadrant σ1 is negative i.e. compressive in nature and σ2 is positive. In third quadrant both σ1 and σ2 are negative i.e. compressive in nature and in last i.e. fourth quadrant σ1 is positive and σ2 is negative. The maximum principle stress is equal to the elastic limit of the material and the material will reach its elastic limit when the stresses (σ1and σ2) go outside the square.
2. Maximum Principle Strain Theory:
This theory also known as Saint Venant’s theory. According to this theory the ductile material starts yielding when the maximum principle strain reaches at that value at which yielding occurs in simple tension or we can say that the minimum principle strain value is equal to the yield point strain in simple compression. This theory is not suitable for the ductile materials because it gives over safe dimensions of the ductile material.
The design equation according to this theory is,
σ1 – µ (σ2 and σ3) ≤ Syt
GRAPHICAL REPRESENTATION:
The shape of the diagram according to the principle stresses is like a Rhombus which is symmetrically placed with respect to the axis. The sign of stresses is same as the previous theory but the shape of diagram is changed.
3. Maximum Shear Stress Theory:
This theory was proposed by Coulombs and Guest. According to this theory the failure of any mechanical component occurs when it is subjected to bi-axial or tri-axial stresses and then the maximum shear stress at any point of the component reaches up to the value which is equal to the maximum shear stress in the standard specimen of the tension test when yielding is start. In the tension test the specimen is subjected to the uniaxial state of stress i.e. σ2 = 0. So the maximum shear is equal to the half of the difference between the maximum and minimum principle stress. Therefore the maximum shear in simple tension is equal to the half of the tensile stress.
Design equation of maximum shear stress theory is
Absolute T max = Syt or (σ1 – σ2)/2 = Syt
This theory is not suitable for ductile materials because it will give over safe design for ductile components. This theory is not applicable to materials subjected to hydrostatic state of stresses, in this case shear stress is almost zero which means the failure in the material will not occurs which is impossible. Graphically a Hexagon represents the stress distribution which shows that the materials will reach its elastic limit when the stresses (σ1and σ2) go outside the region.
4. Total Strain Energy Theroy:
This theory was given by Beltrami Haigh’s. According to this theory the engineering components under the complex stresses fails when the total strain energy in the body is equal to the strain energy at elastic limits in simple tension. This theory states that when a material deformed permanently due to the various stresses. The value of these stresses increase gradually from zero value due to this we can say that the initial strain energy is independent of the nature of stresses and is almost constant.
The design equation according to this theory is
σ12 + σ22+ σ32 – 2µ (σ1σ2 + σ2σ3 + σ3σ1) = (Syt)2
This theory is applicable for those brittle materials who has elastic limit stress in tension and compression are different. The graphical representation of this theory is shown by the Ellipses which are inscribed by the parallelogram. The material mechanical component reaches its elastic limit when the stresses (σ1and σ2) fall outside the ellipse.
5. Maximum Shear Stress Energy Theory:
This theory is also known as the maximum distortion energy theory. This theory was given by M.T. Huber and R. Von Mises. This theory states that the inelastic action at any point in the engineering component starts due to various stresses when the strain energy of distortion per unit volume is absorbed at a point is equal to the strain energy of distortion absorbed per unit volume at any point in a bar which is stressed to the elastic limit under the uniaxial state of stress in the simple tension or compression test. So we can say that the part of the strain energy produce change in the shape of the element is supposed to be completely responsible for the failure of the material by yielding.
This theory is considered as the best and safe among all the theories for designing any mechanical component.
The design equation according to this theory is,
(σ1-σ2)2 + (σ2-σ3)2 + (σ3-σ1)2 = 2 (Syt)2
This theory is not applicable for the brittle materials for which elastic limit stress is different in tension and compression. This theory is also not applicable for hydrostatic state of stress conditions. The graphical representation of this theory is same as the total strain energy theory, both are represented by the Ellipse and the stress variations are also same.
Selection of Theory of Failure:
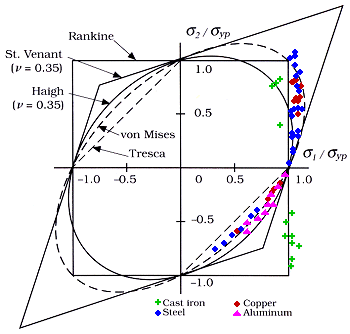
The selection of the theories of failure is depends upon the various factors and different theories are suitable for different materials. The failure of the component is not only depends upon the properties of materials but also on the stress induced in the whole component. All five theories give a safety region the combination of all the theories is as follow
The maximum distortion energy theory is the best theory among all. It provides safe and economical design because the area of the region of this theory is neither too small nor not too large so this is best suitable theory for designing. If the area bounded by the theory of failure curves in a quadrant increases then failure stresses will increases due to this dimension of the component decreases which decrease the safety of the component. So the area of the curve should be within proper limit. Following are the some important points which help us for the selection of theory:
- Maximum distortion energy theory is the best theory of failure for ductile materials because it gives safe and economical design.
- Maximum shear stress theory will give over safe design for ductile materials.
- Maximum shear stress theory and Maximum distortion energy are not suitable for ductile materials under hydrostatic state of stress conditions because shear stress on all the planes passing through is zero or we can say that every plane is principal plane.
- For hydrostatic state of stress conditions maximum principal stress theory and maximum principal strain theory and maximum strain energy theory are best suitable.
- Maximum principal stress theory and Maximum shear stress theory will gives same results in uniaxial state of stress conditions and bi-axial state of stress conditions when principal stresses are like in nature.
This is all about theory of failure. If you have any confusion ask by commenting. If you like this article, don’t forget it on social networks. Subscribe our website for more informative articles. Thanks for reading it.