Today we will learn more about Metacenter and Metacentric Height. In our last article we have discussed about what is buoyancy and buoyancy force which a body experienced when it is submerged or immersed in any fluid. We have also noticed that when we see a ship or boat or any floating body, it oscillate about a point during floating. The point about which it oscillate is known as Metacenter.
What is Metacenter?
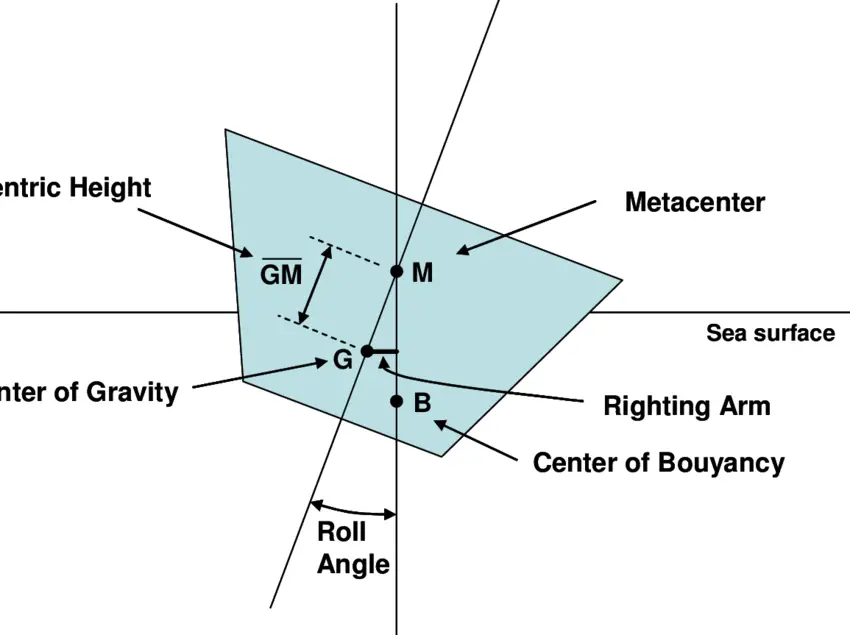
According to the definition “Metacenter is the point, about which a body starts oscillating when it is given a small angular displacement. If the body undergoes angular displacement then the point of intersection of the below mentioned two straight lines is called metacenter
( i ) Axis line of the body passing through the center of gravity and original center of buoyancy (GB) .
( ii ) The vertical line passing through the new center of buoyancy when the body is tilted.
These lines can clearly seen in the diagram.
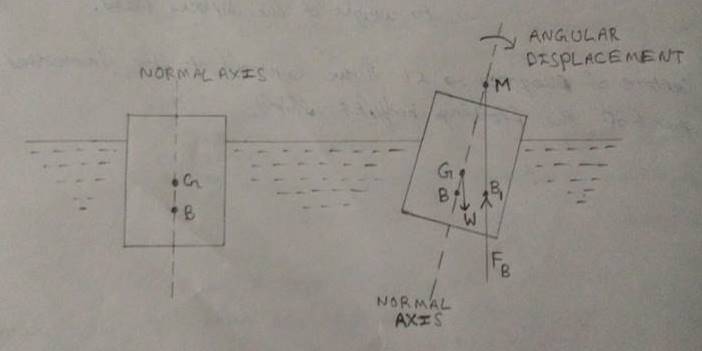
In the above figure point M is the METACENTER.
Metacentric Height:
The distance between the center of gravity of a floating body and the metacenter is called metacentric height.
Metacentric height can be determined by two methods
( i ) Analytical method
( ii ) Experimental method
We will discuss both of these method in detail.
Analytical Method of Finding Metacentric Height:
Let us consider a wedge shaped floating body in equilibrium. The point G be the center of gravity and the point B be the center of buoyancy. If the floating body is given a small angular displacement in the clockwise direction, a new center of buoyancy is formed at point B1 ( i.e., center of buoyancy is shifted from point B to point B1). Here the points G and B lies on the axis line of the floating body, but the point B1 lies on the other vertical line (assume a line and draw in vertical direction). The intersection point of both these lines is called Meta-center (M).
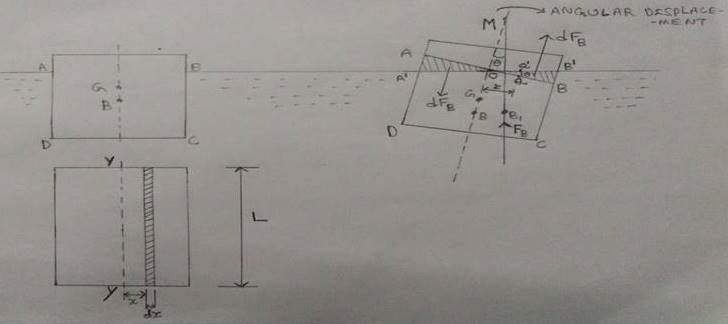
As the body is given small angular displacement in the clockwise direction, the wedge shaped prism on the right side of the axis (region BOBl) submerges into water. The identical wedge shaped prism on the left side of the axis (region AOAl) emerges out of water. These wedges shows the gain of buoyancy force on the right side which is represented by a vertical upward force dFB and loss of buoyancy force (which is equal and opposite force to gained buoyancy force) in the left side which is represented by a downward force dFB. The couple formed due to these two opposite forces tends to rotate the ship in counter clockwise direction. Also the moment caused by the displacement of center of buoyancy from B to B1 is also in the counter clockwise direction. Thus both these couples must be equal.
Consider a small elementary prism QQ1 on the right of the axis at a distance of “x” from point O. (assume, join Q and Q1 to form a triangle QOQ1 )
Height of the prism (h) = x * θ (let distance from Q to Q1 is “ h ” )
Thickness of prism (t) = dx (tan θ = h / x => if θ is small then => θ = h /x )
Length of the floating body = L
Area of the prism (A) = Height * Thickness = x * θ * dx
Volume of prism (V) = Area * Length = x * θ * L *dx
Weight of the prism (W) = Density * Gravitational force * Volume
= ρ * g * x * θ * L * dx
Similarly, if we consider a small prism of thickness “ dx ” at a distance “ x ” from point O towards the left of the axis, the weight of the prism will be
W = ρ * g * x * θ * L * dx .
These two weights are acting in the opposite direction and hence constitute a couple.
Moment of couple = weight of one prism * perpendicular distance between these two weights (forces)
= [ ρ * g * x * θ * L * dx ] * [ x ]
= ρ * g * x * θ * L * dx * x
= 2 ρ g x2 θ L dx
Moment of the couple of whole wedge = ∫ ρ g x2 θ L dx ——–> I
Moment of couple due to shifting of center of buoyancy from B to B1
= FB * BB1 (In the above figure join B and B1, triangle MBB1 is obtained
= FB * BM *θ
now tan θ = ( BB1 / BM ), if θ is small then tan θ = θ
= W * BM *θ ——–> II θ = ( BB1 / BM ) => BB1 = BM *θ )
So FB = W
The above two couples are same. Hence equating equations I and II
W * BM *θ = ∫ ρ g x2 θ L dx
= ρ g θ ∫ x2 L dx
W * BM = ρ g ∫ x2 L dx
In the above figure we can see “ L * dx ” is the elemental area on the water line. So L * dx = dA.
W * BM = ρ g ∫ x2 dA
W * BM = ρ g I ( I = ∫ x2 dA )
( where I = moment of inertia of the sectional area of the plane of body at water surface about the axis Y – Y )
BM = ρ g I / W
W = Weight of the body
= Weight of the fluid displaced by the body
= ρ g * volume of the fluid displaced by the body
= ρ g * volume of the body sub- merged in water
= ρ g * V
BM = ρ g I / ρ g V = I / V
GM = BM ± BG
+ve sign if G is lower than B.
-ve sign if G is higher than B.
Experimental Method of Finding Metacentric Height:
Let us consider a floating vessel with a known weight of w1 over it, at its center. If the weight w1 is shifted by a distance “ x ” across the vessel. The vessel is tilted by an angle θ. This angle of tilt may be measured by means of plumb bob method or protractor attached on the vessel. As the vessel is tilted its center of gravity and center of buoyancy are also shifted from G to G1 and B to B1.
W = weight of vessel including w1
G = center of gravity of the vessel
B = center of buoyancy of the vessel
θ = angle of tilt
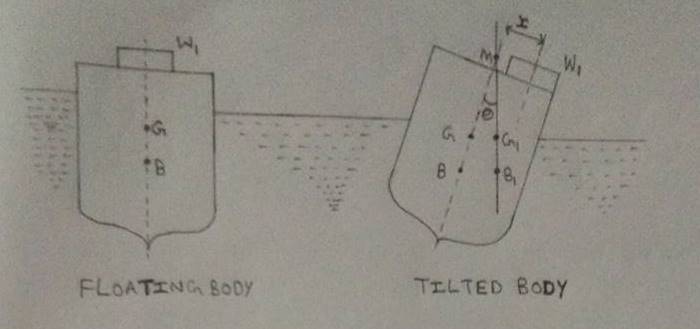
Moment due to movement of w1 = w1 * x
( join GG1, triangle GMG1 is formed )
Moment due to change of G = GG1 * W = W * GM tan θ (tan θ = GG1/GM)
Under equilibrium, the moment caused by the movement of load w1 through a distance “ x ” must be equal to the moment caused by the shift of center of gravity from G to G1.
w1 * x = W * GM tan θ
Metacentric height (GM) = ( w1 * x ) / ( W tan θ )
If L = length of the plumb bob
d = displacement of plumb bob
then tan θ = d / L
Metacentric height GM = ( w1 x L ) / ( W d )
Oscillation (Rolling) Of A Floating Body:
Whenever a floating body in the liquid is given small angular displacement, it starts oscillating about its metacenter (M) like the same manner as of a pendulum oscillates about its point of suspension.
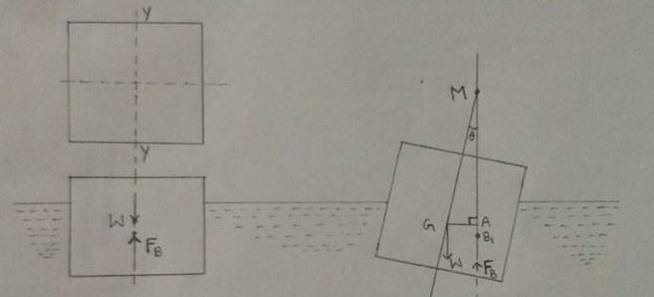
Let W = Wight of floating body
θ = Angle through which the body is depressed ( in radians )
α = Angular acceleration of the body ( in radians/sec2 )
T = Time of rolling ( i.e., one complete oscillation ) ( in seconds )
k = Radius of gyration about center of gravity ( G )
I = Moment of inertia of the body about its center of gravity ( G ) = ( W/g ) k2
GM = Metacentric height of the body
Whenever the force that causes angular displacement is removed, the only force acting on the body is due to the restoring couple, due to the weight (W) of the body and the force of buoyancy FB.
Restoring couple = W * Distance GA ( From triangle GAM, sin θ = )
= W * GM sin θ
(This couple tries to decrease the angle, so as θ is small sin θ = θ )
Restoring couple = W * GM * θ ——————> I
Angular acceleration of the body α = – ( d2θ / dt2 )
( -ve sign indicates that the force is acting in such a way that it tends to decrease the angle θ. )
Torque due to inertia = moment of inertia * angular acceleration
= I * α
= – ( W / g ) k2 * ( d2θ / dt2) ———> II
Equating equations I and II
W * GM * θ = – ( W / g ) k2 * ( d2θ / dt2)
( W / g ) k2 * ( d2θ / dt2) + W * GM * θ = 0
Dividing the equation with “ W ”
( k2 / g ) * ( d2θ / dt2) + GM * θ = 0
Again dividing the equation with ( k2 / g )
( d2θ / dt2) + ( GM * g * θ ) / k2 = 0
The obtained above equation is in the form of “Differential Equation of Second Degree”, solution will be
θ = C1 sin [ ( ) * t ] + C2 cos [ ( ) * t ] ————> III
Where C1 and C2 are constants of integration.
The values of C1 and C2 are obtained from the following boundary conditions :
( i ) At t = 0, θ = 0
By substituting t = 0 and θ = 0 in equation III,
We get C2 = 0
( ii ) At t = ( T/2 ), θ = 0
By substituting t = 0 and θ = 0 in equation III
0 = C1 sin [ ( ) * ( T/2 ) ]
Here C1 cannot be equal to zero, so the other alternative is
sin [ ( ) * ( T/2 ) ] = 0 ( sin Π = 0 )
( ) * ( T/2 ) = Π
T = 2 Π
Time period of oscillation ( T ) = 2 Π
Conditions Of Equilibrium Of Floating and Sub-merged Bodies:
For a floating or submerged body it is said to be in stable if the body comes back to its original position after a slight disturbance. The buoyant force should be equal to weight of the body, and the center of buoyancy and center of gravity should be on the same vertical center line for a body to be in equilibrium.
For a sub-merged body, weight of the body should be equal to buoyant force.
- stable equilibrium : when the body is given a slight angular displacement, then a restoring couple is formed by the buoyant force and weight of the body to return to its original position.
In case of sub-merged bodies, center of buoyancy is above center of gravity.
In case of floating bodies, metacenter is above center of gravity. - Unstable equilibrium : An over-turning couple is formed by the buoyant force and weight of the body, thus the body does not return to its original position. ( If it is a floating body, it can sink into the fluid.)
In case of sub-merged bodies, center of buoyancy is below center of gravity.
In case of floating bodies, metacenter is below center of gravity. - Neutral equilibrium : when the body is given a slight angular displacement, occupies a new a new position and remains at rest in the new position.
In case of sub-merged bodies, center of buoyancy and center of gravity are at same point.
In case of floating bodies, metacenter and center of gravity coincide.
NOTE :
- When an object is submerged, the volume of water displaced must be equal to the volume of object submerged regardless of its shape.
- A floating object displaces fluid based on its mass.
- A sinking object displaces fluid based on its volume.
- Weight of the fluid displaced by the immersed body is equal to the buoyant force on the submerged body. This principle is useful for determining the volume and therefore the density of an irregularly shaped object by measuring its mass in air and its effective mass when submerged in water.
- Buoyancy force depends upon the density of the fluid ( does not depend upon the density of object ) .
Prism : A solid geometric figure whose two ends are similar, equal, and parallel rectilinear figures and whose sides are parallelograms.
Couple : When two forces of equal magnitude opposite in direction and acting along parallel straight lines form a couple. The perpendicular between the two force forming a couple is called the arm of the couple.
Moment : The turning effect of a force is known as moment. Moment is the product of the force multiplied by the perpendicular distance from the line of action of the force to the point.
This is all about metacenter and metacentric height. if you have any doubt regarding this article ask by commenting.

From which book I can get this?. It is urgent